One important contribution of James Buchanan and Gordon Tullock’s (1999) The Calculus of Consent, published in 1962, is their analytical framework which can be used to determine the optimal majority in a democracy or in general when collective choice needs to be decided via a voting process. Starting with two interdependent costs—external costs, defined as the externality imposed on individuals if the policy they oppose is passed, and transaction costs (or decision-making costs), which are the costs of time and effort (or the costs of bargaining) required for a group of individuals to reach an agreement for a collective choice—Buchanan and Tullock formulated the problem as the minimization of the total social costs, which are the sum of external costs and transaction costs.

Despite the fact that Buchanan and Tullock were aware that the functions of external costs and transaction costs could take any form, the convexity of the total social costs curve was generally assumed. This assumption in turn led to a guarantee of the interiority and the uniqueness of the optimal majority. This article points out that in certain hypothetical cases, the optimal majority might be noninterior, nonunique, or both.

The first section readdresses the Calculus of Consent model and explains why Buchanan and Tullock’s primary construction of external costs and transaction costs guaranteed an interior optimal majority. The second section points out the scenarios in which the convexity of the external costs curve and transaction costs curve, and thus of the total social costs curve, is not satisfied. It focuses on the case where the total social costs curve is strictly concave and as a result the optimal majority is a corner solution. This result implies extreme cases in which either the unanimity rule is needed or private action is strictly preferred to collective action, with the former being illustrated by the case of democratic centralism. The third section briefly examines the case where the existence of multiple optimal majorities is a possibility. The proofs for all the results here are omitted, since they are standard in optimization theory.

The article contributes two theoretical insights: First, when individual voters are heterogeneous, private action may end up being a better solution than collective choice unless unanimity is satisfied. Second, in a situation with multiple optimalities, finding a minimand no longer serves as a sufficient criterion to determine the size of the optimal majority. The implication is that when there exists a set of possible optimalities from which one must be selected, something other than a consideration of optimality must guide political bargaining. Hence, the ambiguity in determining the optimal majority requires a criterion beyond analytical optimality to justify the majority rule.

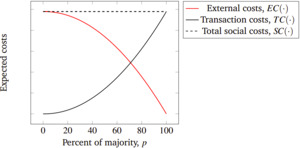
In the standard setup, the process of reaching collective agreements can be seen as a Coasean bargaining process (Aligica, Boettke, and Tarko 2019, 50–51). With this logic, the process entails two types of costs: external costs, defined as “the costs that [an individual] expects to endure as a result of the actions of others to the number of individuals who are required to agree before a final political decision is taken for the group”; and transaction costs, which are “[the cost of] time and effort . . . which is required to secure [collective] agreement” (Buchanan and Tullock 1999, 64, 68). The external costs function \(EC( \cdot )\) is generally a decreasing function, represented by the red curve in figure 1. Meanwhile, the transaction costs function \(TC( \cdot )\) is increasing, as shown by the black curve. Since there are no external costs under the unanimity rule and no transaction costs associated with zero agreement, \(EC(100) = TC(0) = 0\). With the objective of minimizing the total social costs \(SC( \cdot )\), defined as \(SC( \cdot ) = EC( \cdot ) + TC( \cdot )\), the optimal majority required for collective action is thus the minimand \(p^{*}\) of the function \(SC( \cdot )\);[1] this is illustrated by the black dot in figure 1.

Figure 1
Figure 1.The Calculus of Consent model with convex costs

Although Buchanan and Tullock were aware that in reality the external and transaction costs curves are not always as well behaved as depicted, their primary construction of these functions assumed the following:

\[\frac{\partial EC}{\partial p} < 0;\frac{\partial TC}{\partial p} > 0;\frac{\partial^{2}EC}{\partial p^{2}} > 0;\frac{\partial^{2}TC}{\partial p^{2}} > 0.\]

It might be argued that these assumptions came from the fact that Buchanan and Tullock’s central focus was on the decision-making of the entire collectivity, without placing much emphasis on the marginal voter. Notwithstanding their recognition of the importance of cost analysis when it comes to individual voters—they wrote, for example, that “[the individual’s] final decision must rest upon a comparison of these costs with those expected to be imposed on him as a result of collective organization itself” (Buchanan and Tullock 1999, 63)—their model analyzed total costs almost exclusively, while marginal costs took a back seat. For the present, we define “marginal external costs” to be the external costs imposed on the marginal voter, with “marginal transaction costs” defined similarly. As we shall see, the introduction into the model of marginal external costs and marginal transaction costs generates further complications in the behavior of the \(EC( \cdot )\) and \(TC( \cdot )\) functions.

As can be seen from figure 1, in the original setup of the model, marginal external costs are decreasing and marginal transaction costs are increasing. In other words, \(EC( \cdot )\) and \(TC( \cdot )\) are convex. Formulating the model in terms of convexity allows us to relax the assumptions of the monotonicity of \(EC( \cdot )\) and \(TC( \cdot )\), since it is possible to show that even the first two of the four above assumptions could be violated (Caplin and Nalebuff 1988). Given the convexity of \(EC( \cdot )\) and \(TC( \cdot )\), we have the following result:

Result 1: With \(EC( \cdot )\) and \(TC( \cdot )\) being (strictly) convex, the sum \(SC( \cdot ) = EC( \cdot ) + TC( \cdot )\) is also (strictly) convex, and the (unique) minimand \(p^{*}\) of \(SC( \cdot )\) is in the interior.

It is clear that when external costs and transaction costs are well behaved, we always have a desired interior optimal majority between 0 percent and 100 percent. When external costs are prohibitive, a larger majority is required, and similarly when the transaction costs of persuading voters are high, the optimal majority tends to be smaller. Although there were times when Buchanan and Tullock relaxed the convexity of external costs, in their analysis they generally treated the total social costs function \(SC( \cdot )\) as convex to guarantee a unique interior solution.

As we will see in the following sections, when cases in which either of the cost curves is concave arise, neither an interior solution nor the uniqueness of the solution can be guaranteed.

Concave Social Costs and Noninterior Solutions

Paul Aligica, Peter Boettke, and Vlad Tarko (2019, 50–51) correctly pointed out that the level of optimal majority is determined by the shapes of \(EC( \cdot )\) and \(TC( \cdot )\). Indeed, in the literature there have been examples where the costs curves do not behave as depicted above: Buchanan and Tullock (1999, 73–74) relaxed the convexity of \(EC( \cdot )\); Dennis Mueller (2003, 76–77) showed a kink in \(TC( \cdot )\) at the simple majority \(p = 50\%\); and Andrew Caplin and Barry Nalebuff (1988) showed that the \(TC( \cdot )\) curve might not even be an increasing function (illustrated in Mueller [2003, 103]). Although all these authors recognized that odd behaviors of the external and transaction costs curves might exist, they all shared a common assumption of the convexity of the total social costs curve \(SC( \cdot )\). Unfortunately, the convexity of \(SC( \cdot )\) can never be guaranteed, since once either the external costs curve or the transaction costs curve is not well behaved, the shape of the total social costs curve is greatly altered.

In general, without knowing the exact specification of any two functions, we cannot say anything about the form of the function of their sum. The function of their sum could be globally concave, globally convex, or neither. In other words, we have the following result:

Result 2: Given two functions \(EC( \cdot )\) and \(TC( \cdot )\), when one function is convex and the other is concave, the convexity of \(SC( \cdot ) = EC( \cdot ) + TC( \cdot )\) is inconclusive.[2]

In other words, when either \(EC( \cdot )\) or \(TC( \cdot )\) is a concave function, the total social costs curve \(SC( \cdot )\) can take any shape, which leads to an indeterminacy of the optimal level of majority. In fact, concavity of \(EC( \cdot )\) or \(TC( \cdot )\) is not a theoretical impossibility, since it is feasible to conceive of increasing marginal external costs as well as decreasing marginal transaction costs. As pointed out by Buchanan and Tullock (1999, 73–74), there exist cases where individuals’ cost structure is significantly adjusted, and one of them is a major interruption in the structure of property rights:

Collective or public decisions [could possibly] modify or restrict the structure of individual human or property rights after these have once been defined and generally accepted by the community. . . . In such cases [the voter] will tend to place a high value on the attainment of his consent, and he may be quite willing to undergo substantial decision-making costs in order to insure that he will, in fact, be reasonably protected against confiscation. In terms of our now familiar diagrams . . . the upper curve, that of external costs, remains relatively high throughout its range over the various decision-making rules until it bends sharply toward the abscissa when near unanimity becomes the rule.

That is to say, marginal external costs might be increasing, making the \(EC( \cdot )\) function concave, as illustrated by the red curve in figure 2.

There is no reason to believe that marginal transaction costs are always increasing either. One potential candidate for making marginal transaction costs decrease as the level of majority increases is the spillover effect of the votes themselves. A marginal voter might feel resistance toward a low percentage of majority, and thus it is harder to convince him when the percentage is low. Conversely, the probability that he will agree on a policy increases as the number of his fellow voters who agree increases. Thus, marginal transaction costs decrease, making the transaction costs curve concave, as shown by the black curve.

Figure 2
Figure 2.The Calculus of Consent model with concave costs

Factors that influence this spillover effect include but are not limited to (1) the timing of the vote; (2) the information about other voters available to a marginal voter; and (3) the coalitions formed between voters who share the same political position. For example, the more a voter knows that his fellow voters (possibly within the same political coalition) are likely to agree with him on a certain policy, the easier it is to convince him, and vice versa. The spillover effect on marginal transaction costs can indeed be neglected if we suppose that individual voters are homogeneous; however, this assumption is clearly not a reasonable one. More to the point, as Sevgi Yuksel (2021) has shown, when heterogeneous voters specialize in the issues most important to them, the degree of political polarization increases accordingly. As a result, we should expect them to have the tendency to rely more on the group that shares their political positions. In short, in the presence of heterogeneous voters, it is possible to have a spillover effect leading to the concavity of \(TC( \cdot )\).

As mentioned before, applications of the Calculus of Consent model shared a common assumption of the convexity of \(SC( \cdot )\), but result 2 shows that it is completely possible to have a concave function for \(SC( \cdot )\) when either \(EC( \cdot )\) or \(TC( \cdot )\) is nonconvex. Here the focus is on the simple case where both external costs and transaction costs are concave, yielding the following result:[3]

Result 3: With \(EC( \cdot )\) and \(TC( \cdot )\) being (strictly) concave, the sum \(SC( \cdot ) = EC( \cdot ) + TC( \cdot )\) is also (strictly) concave, and the (unique) minimand \(p^{*}\) of \(SC( \cdot )\) is a corner solution.

To put it differently, with increasing marginal external costs and decreasing marginal transaction costs, the optimal majority is either \(p^{*} = 0\%\) or \(p^{*} = 100\%\). At \(p^{*} = 0\%\), \(SC(0) = EC(0) + TC(0) = EC(0)\text{,}\) and at \(p^{*} = 100\%\), \(SC(100) = EC(100) + TC(100) = TC(100)\). To determine the optimal majority, three cases follow:

Corollary: 1. If \(EC(0) < TC(100)\), the optimality is \(p^{*} = 0\%\). In other words, a complete rejection of collective action in favor of private choice is socially optimal.

2. If \(EC(0) > TC(100)\), the optimality is \(p^{*} = 100\%\). In other words, the unanimity rule is socially optimal.

3. If \(EC(0)\ = \ TC(100)\), multiple optimalities arise, a situation discussed in the next section.

This result implies that when individuals’ cost structure is not well behaved, because of individual preferences, heterogeneity of voters, or institutional-organizational factors, we end up on either extreme. Case 1 could be explained quite intuitively: when voters are highly heterogeneous but cast their votes depending on other voters, or when preferences among different political coalitions are extremely polarized, the transaction costs of reaching a collective agreement are highly prohibitive, exceeding the external costs. Consequently, voters are likely to abandon collective choice in favor of private ones. Or, alternatively, each political coalition might employ polycentric solutions within its own group, as polycentric rules are generally less costly than collective, monocentric ones (Ostrom 1990, chap. 4).

Interestingly, case 2 is also not rare if we look at voting within the system of democratic centralism in Communist regimes, under which political proposals are passed with almost absolute unanimity. This is not a coincidence, since democratic centralism satisfies most of the conditions stated above: (1) property rights in Communist regimes are not protected, with constant changes in legislation; (2) information about individual voters is quasi-public within the Communist party itself; and (3) members of the Communist party usually form different coalitions, from the local level up to the central politburo. The second condition is a prominent characteristic of democratic centralism as laid down in 1901 by Lenin (2013, chap. 1): that members of the Communist party ought to be loyal to the party’s platform. The observability of the votes serves as a constraint assuring that the party’s members do not vote against the platform. This constraint is present at all levels of election, from within the local committee up to the top level. As Communist party members face extremely high losses for going against the platform, whether it be in terms of economic benefits or of their political careers, there are substantial external costs for not enacting Communist agendas and policies. Hence the extensive record of unanimity across different Communist regimes when it comes to voting should not be a surprise (Saxonberg 2013).[4]

Multiple Optimalities

The previous section leaves unexplored case 3, when \(EC(0)\ = \ TC(100)\). As mentioned above, in general this is when multiple optimal majorities arise. In the setup of their model, Buchanan and Tullock assumed the exogeneity of the institutional structure as well as of its organizational decision-making. This undoubtedly simplified the analysis, as long as the optimal majority can be uniquely determined. In the case where multiple optimalities exist, institutional-organizational factors play a role in determining the optimal majority.

There are many ways to construct the external costs and transaction costs curves to yield multiple percentages that minimize the total social costs curves; the setup in case 3 in the second section, with \(EC(0) = \ TC(100)\text{,}\) is one of them. In general, we can conceive of cases where \(EC( \cdot )\) and \(TC( \cdot )\) are convex but not strictly convex, or where they are quasi-convex, leading to multiple minimands \(p^{*}\). This article presents the simplest case, assuming that both \(EC( \cdot )\) and \(TC( \cdot )\) are strictly monotonic and thus nonconstant. Suppose that, given an \(EC( \cdot )\) curve, we can assume the marginal transaction costs of a marginal voter to be perfectly negatively correlated to his corresponding marginal external costs. Mathematically,

\[\frac{\partial TC}{\partial p} = - \frac{\partial EC}{\partial p} \Longleftrightarrow \frac{\partial EC}{\partial p} + \frac{\partial TC}{\partial p} = 0.\]

This hypothetical assumption of the symmetry between external costs and transaction costs is based on our conceiving the costs to convince a marginal voter to be equal to the costs imposed (and thus compensation required) on that individual voter if the policy is passed, assuming there are no other costs of time and effort. With \(SC( \cdot ) = EC( \cdot ) + TC( \cdot )\), we can thus derive

\[\frac{\partial SC}{\partial p} = \frac{\partial EC}{\partial p} + \frac{\partial TC}{\partial p} = 0.\]

Figure 3
Figure 3.The Calculus of Consent model with multiple optimalities

This implies that, when we have a symmetry between \(EC( \cdot )\) and \(TC( \cdot )\), the total social costs function \(SC( \cdot ) = EC( \cdot )\ + TC( \cdot )\) is a constant function, as shown in figure 3. Consequently, any percentage of the majority is an optimal majority because they all minimize the total social costs function. Again, although the assumption of constant total social costs is not realistic, there exist many possibilities that give multiple minimands for the total social costs function. The implication is that optimizing the total social costs no longer serves as a sufficient criterion for determining the optimal majority. When this happens, (1) the optimality is determined by other specific objectives within the organization, (2) we must rely on other normative standards, (3) there must be a secondary bargaining process within the organization to determine the optimal majority, or (4) any possible combination of the first three options can be applied. In any case, institutional determinants will become endogenous and must be taken into account.

It should be noted that option 3 is particularly important because it is evident in the real world that collective bargaining is usually not a static process or a one-shot game. The necessity of a secondary bargaining process suggests a potential for applying sequential bargaining and dynamic game theory to model collective action; Jeffrey Banks and John Duggan (2000) made an attempt, but their analysis remains static. Furthermore, the existence of multiple optimal majorities also highlights the fact that due to different layers of complexity in the institutional-organizational structure of the collective, it is sometimes difficult to determine the level of majority that is socially optimal.

Conclusion

This article presents several hypothetical cases in which the optimal majority in the Calculus of Consent model is neither interior nor unique. The former cases serve to illustrate that, given some reasonable settings, the optimal majority might fall to either extreme, such that voters would demand complete unanimity or opt for private choice. The latter cases emphasize the difficulty, and sometimes ambiguity, of determining the optimal level of majority when multiple optimalities arise. The essence of this difficulty is the fact that minimizing total social costs no longer serves as a sufficient criterion to determine the level of the optimal majority. When this happens, the institutional-organizational structure of the collective becomes an important factor in determining such an optimality—that is to say, we need a criterion beyond analytical optimality to justify the majority rule. Moreover, the necessity for secondary collective bargaining to determine the optimal majority opens the door for future research that applies sequential or dynamic bargaining to collective choice.

  1. Throughout this article, we define “optimal majority” purely in the analytical sense—as the solution to the minimization problem—without referring to other standards for optimality. We also assume for the sake of simplicity that both \(EC( \cdot )\) and \(TC( \cdot )\) are twice differentiable. Analyzing the concavity of a function, however, does not require such an assumption. The differentiability of the functions here could easily be relaxed and the main analysis of the article still remain intact.

  2. The converse was proved by Alan Yuille and Anand Rangarajan (2003), such that any function \(f \in \mathcal{C}^{2}\lbrack a,b\rbrack,\forall a,b\mathbb{\in R}\) could be decomposed into a sum of a convex and a concave function.

  3. One example in which concavity of only one function is sufficient to make \(SC( \cdot )\) concave is \(EC( \cdot ) = f( \cdot ) - g( \cdot ),TC( \cdot ) = g( \cdot )\), with concave \(f\), convex \(g\), and concave \((f - g)\). Then \(EC( \cdot ) + TC( \cdot ) = f( \cdot ) - g( \cdot ) + g( \cdot ) = f( \cdot )\), which is a concave function.

  4. It should be clarified that in Communist systems, the relevant votes are only those of the Central Committee, which is composed of Communist party members who hold power. Hence, while the above does not suggest from the social perspective that unanimity should be adopted, it is still desirable from the perspective of the party or the politburo itself to have unanimity. Lenin (2013, chap. 1) also considered unanimity to be a defining characteristic of a Communist party.